A137
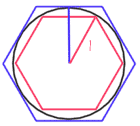 |
計算方法はいくつかあるのですが、その中でも分かりやすいのは 数学者アルキメデスが考えた計算方法です。 その方法とは、円に内接する多角形と外接する多角形を考えるものです。 例えば左図のように、半径1の円に内接・外接する 正六角形を考えてみましょう。 この場合、内接する正六角形(赤)の外周は 6、 外接する正六角形(青)の外周は 4√3 と 高校の数学レベルの知識があれば求められます (左図で円の中心から出ている2直線は共に長さ1ですね)。 また、円周は 2πr = 2π なので、6 < 2π < 4√3 と判明します。 すべて2で割ると、3 < π < 2√3 という結果になりました。 2√3 は約 3.46 なので、πは3より大きく、3.46より小さい数字 であることが分かります。間違いありませんね。 そしてこの多角形の辺の数を増やしていけばどんどん 円に近くなり、正確なπの値に近づく、というわけです。 |